🧮 Choosing between MAE, MSE and RMSE

One common task in Data Science is solving regression problems. Several metrics are available to choose from when evaluating the performance of regression models. The most standard ones are Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE). Each of these metrics has strengths and weaknesses; choosing the right one depends on the problem and context. But what do they mean, and how do they differ?

In this blog post, I will explain the meaning and intuition behind these metrics and provide some guidance on when to use which one.

Mean Absolute Error (MAE)

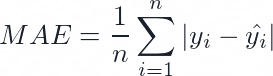
MAE is the most straightforward and intuitive metric among the three. It is calculated by taking the average of the absolute values of the errors, which are the differences between the predicted and actual values. For example, if you have a dataset with five observations and your model predicts [12, 13, 14, 15, 16] while the actual values are [10, 11, 12, 13, 14], then the MAE is (|10-12| + |11-13| + |12-14| + |13-15| + |14-16|) / 5 = 2. MAE measures how close the predictions are to the actual values on average, regardless of the direction of the error. It is advantageous when the outliers in the dataset can significantly impact the model's performance. This is because MAE is less sensitive to outliers than MSE or RMSE. In addition, because MAE is calculated based on absolute differences, it measures how far off the predictions are on average, which can help interpret the model's performance.

The MAE has some nice properties:

• It is easy to understand and interpret.
• It is robust to outliers, meaning that it is not affected by extreme errors.
• It has the same unit as the target variable, making it easy to compare. The MAE tells us that, on average, our predictions are off by two units from the actual values.

However, the MAE also has some drawbacks:

• It does not penalise large errors as much as small errors, meaning that it might not reflect the true accuracy of the model.
• It is not differentiable at zero, meaning optimising using gradient-based methods is harder.

Mean Squared Error (MSE)

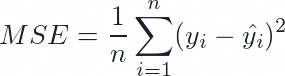
MSE stands for Mean Squared Error, and it is calculated as the average of the squared differences between the actual and predicted values. Using the same example as above, the MSE is ((10-12)^2 + (11-13)^2 + (12-14)^2 + (13-15)^2 + (14-16)^2) / 5 = 4. MSE measures how close the predictions are to the actual values on average, but it gives more weight to large errors than small ones. This means that MSE is more sensitive to outliers and can be useful in identifying models that make large mistakes.

The MSE has some advantages over the MAE:

• It penalises large errors more than small ones, reflecting the true accuracy of the model better.
• It is differentiable everywhere, meaning optimising using gradient-based methods is easier.

However, the MSE also has some disadvantages:

• It is sensitive to outliers, meaning that extreme errors can skew it.
• It has a different unit than the target variable, making it harder to compare.

Root Mean Squared Error (RSME)

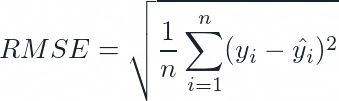
RMSE stands for Root Mean Squared Error, and it is calculated as the square root of the MSE. Using the same example above, the RMSE is sqrt(MSE) = sqrt(4) = 2. RMSE has the same unit as the actual and predicted values, making comparing them easier. RMSE also measures how close the predictions are to the true values on average, but it gives more weight to large errors than small ones. RMSE is one of the most common metrics in regression because it is easy to differentiate and use with gradient-based methods.

The RMSE has some benefits over both MAE and MSE:

• It has the same unit as the target variable, like MAE, but not too different, like MSE.
• It penalises large errors more than small errors like MSE, but not too much like MSE.

However, the RMSE also has some drawbacks:

• It is still sensitive to outliers like MSE.
• It is not easily interpretable like MAE.

So, how do you choose between MAE, MSE and RMSE? There is no definitive answer to which metric to use for regression problems. It depends on your data, your model and your objective. Here are some general guidelines:

• If you want a simple and intuitive metric robust to outliers, use MAE.
• If you want a metric that reflects the true accuracy of your model and is easy to optimise, use MSE.
• If you want a compromise between MAE and MSE, you can use Root Mean Squared Error (RMSE) which is more sensitive to outliers than MAE but less sensitive than MSE.
• If you care more about small errors than large ones, or if your data has many outliers, you might prefer MAE over MSE or RMSE.
• If you care more about large errors than small ones or want to penalise models that make large mistakes, you might prefer MSE or RMSE over MAE.
• If you want a metric with the same unit as your actual and predicted values, you might prefer RMSE over MSE or MAE.
• If you want a metric that is easy to differentiate and use with gradient-based methods, you might prefer MSE or RMSE over MAE.