🔮 Implementing k-Nearest Neighbours from Scratch
The k-Nearest Neighbour is a supervised learning algorithm that is simple and quick to implement and can be used in classification and regression problems.
Let us imagine that we are given the task of identifying the species of penguins from the Antarctica region. How would we solve this problem?
Table of Contents:
Introduction
In this post, we will implement a k-Nearest Neighbour classification algorithm from scratch in Python to train a classifier to identify the species of penguins. One could believe that animals from the same species share similar features. The k-Nearest Neighbour algorithm assumes that similar things co-exist near each other. Examples are classified based on the majority class of their neighbours.
We will be using the palmerpenguins dataset, a great alternative to the famous iris dataset. It contains 344 entries. There are three different species of penguins in this dataset, collected from 3 islands in the Palmer Archipelago, Antarctica.
k-Nearest Neighbours
The k-Nearest Neighbour classification is a type of instance-based learning. It relies on a distance metric for classification. The output is computed from a majority vote of the nearest neighbours of each data point. Therefore an unseen observation is assigned the most common class among its k nearest neighbours. It also does not construct any general internal model during the fit. Instead, it simply stores the instances of the training data.
The number of neighbours is defined by k, which is a positive integer, usually small. When k = 1, the unseen observation takes the class of that single nearest neighbour.
Since this algorithm relies on distance, if the features have different units of dimension or scaling, then normalising the training data can significantly improve its performance.
The basic algorithm uses uniform weights, meaning that each neighbour vote contribution is the same, and as I mentioned before, the majority vote determines the class. Another possible technique can assign distinct weights to the contributions of the neighbours so that the closer neighbours have more impact on the average than more distant ones. For example, a common strategy for setting the weights consists of giving each neighbour a weight of 1/d, where d is the distance to the neighbour.
The algorithm works as the following:
- Load the training data
- Set the k for the number of neighbours
- Calculate the distance between the query data point and each data point from the training data.
- Store and sort the list of calculated distances by ascending order.
- Fetch the first k entries from the ordered list.
- Get the labels of the selected entries.
- Return the most common label.
In a regression problem, the average of the neighbours' values is calculated instead of the most common label.
Selecting the optimal k value
The best choice of value for k depends upon the data. Generally speaking, higher values of k reduce the noise on the classification, but the boundaries between classes are slimmer. In comparison, smaller values of k can lead to less reliable predictions. It is a good practice to test different values using hyperparameter optimisation to find a good value for k. When using the majority vote technique, an odd k value is usually used to ensure a tiebreak.
Pros
- The algorithm is simple to interpret and easy to implement.
- It does not need to build a model during the training phase.
Cons
- However, it can become slower as the number of examples or the number of features increase.
Code Implementation
Now, we will write from scratch the k-Nearest Neighbours algorithm. This implementation will be a simple version where the weights are uniform.
A few code blocks with intermediary steps are hidden in collapsable sections.
Import some packages: numpy, pandas, matplotlib and sklearn helpers.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# Set seed for reproducibility
SEED = 42
np.random.seed(SEED)
We will use the Euclidean distance as the distance metric for our algorithm. The Euclidean distance is a commonly used distance metric for continuous values.
def euclidean_distance(x1, x2):
return np.sqrt(np.sum((x1 - x2)**2))
We will create a KNN class to define the behaviour of our model. It will take the k number of neighbours as an argument, and it will implement a fit and predict methods.
class KNN:
def __init__(self, n_neighbors=3):
self.n_neighbors = n_neighbors
def fit(self, X, y):
self.X_train = X
self.y_train = y
return self
def predict(self, X):
return np.array([self._predict(x) for x in X])
def _predict(self, x):
# 1. Compute distances between x and all examples in the training set
distances = [euclidean_distance(x, x_train) for x_train in self.X_train]
# 2. Sort by distance and return indices of the first k neighbors
k_idx = np.argsort(distances)[:self.n_neighbors]
# 3. Extract the labels of the k nearest neighbor training samples
labels = self.y_train[k_idx]
# 4. Return the most common class label
labels_count = np.bincount(labels)
return np.argmax(labels_count)
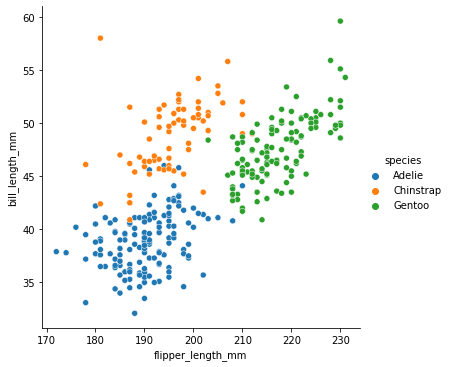
Next, we load the data, drop a few examples with missing values and do some data visualisation.
data = sns.load_dataset('penguins').dropna()
sns.relplot(x='flipper_length_mm', y='bill_length_mm', hue='species', data=data)
Before training the model, we will apply one-hot encoding to the non-numerical features, and label encode our target variable.
data = pd.get_dummies(data, columns=['island', 'sex'])
data['species'], _ = data['species'].factorize()
data.head()

Split the data with a ratio of 80% train data and 20% test data.
y = data['species'].to_numpy()
X = data.drop('species', axis=1).to_numpy()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,
random_state=SEED)
Standardize both train and test data since the KNN algorithm uses a distance metric and is affected by the scale of the features.
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
Finally, we will fit a KNN model with k equal to three and make our predictions on the test set, and then we will evaluate the performance of our model by measuring the accuracy score. We will also create a KNN classifier using sklearn to compare how well our basic model delivers.
clf = KNN(n_neighbors=3).fit(X_train, y_train)
y_pred = clf.predict(X_test)
print(f"Accuracy: {accuracy_score(y_test, y_pred):.3f}")
# Accuracy: 0.985
from sklearn.neighbors import KNeighborsClassifier
sklearn_knn = KNeighborsClassifier(n_neighbors=3).fit(X_train, y_train)
y_pred = sklearn_knn.predict(X_test)
print(f"Accuracy: {accuracy_score(y_test, y_pred):.3f}")
# Accuracy: 0.985
Summary
The k-Nearest Neighbours (KNN) is a simple supervised algorithm used in classification and regression problems. We have implemented a basic version of a KNN classifier to help us predict the species of penguins from Antarctica. We achieved an ~98% accuracy score which is a pretty good result for the task at hand. Implementing machine learning algorithms from scratch is, in my opinion, an excellent way to learn the inner works of the different machine learning techniques.
You can find the complete code in this repository.
Thank you for taking the time to read. You can follow me on Twitter, where I share my learning journey. I talk about Data Science, Machine Learning, among other topics I am interested in.
